Graph - basic manipulation

This notebook illustrates the basic functionality of pyrigi.graph.Graph. It can be downloaded here.

from pyrigi import Graph

An easy way to construct a graph is to provide the list of its edges:

G = Graph([(0, 1), (1, 2), (2, 3), (0, 3)])
G

Graph.from_vertices_and_edges([0, 1, 2, 3], [(0, 1), (0, 3), (1, 2), (2, 3)])

Edges and vertices can be added:

G.add_vertices([0, 2, 5, 7, 'a', 'b'])
G.add_edges([(0, 7), (2, 5)])
G

Graph.from_vertices_and_edges([0, 1, 2, 3, 5, 7, 'a', 'b'], [(0, 1), (0, 3), (0, 7), (1, 2), (2, 3), (2, 5)])

or removed:

G.delete_vertex('a')
G

Graph.from_vertices_and_edges([0, 1, 2, 3, 5, 7, 'b'], [(0, 1), (0, 3), (0, 7), (1, 2), (2, 3), (2, 5)])

G.delete_vertices([2, 7])
G

Graph.from_vertices_and_edges([0, 1, 3, 5, 'b'], [(0, 1), (0, 3)])

G.delete_edges([(0, 1), (0, 3)])
G

Graph.from_vertices_and_edges([0, 1, 3, 5, 'b'], [])

There are also other ways how to construct a graph:

import pyrigi.graphDB as graphs
graphs.Complete(4)

Graph.from_vertices_and_edges([0, 1, 2, 3], [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)])

graphs.Complete(3, ['a', 1, (1.2)])

Graph.from_vertices_and_edges(['a', 1, 1.2], [('a', 1), ('a', 1.2), (1, 1.2)])

from sympy import Matrix
Graph.from_adjacency_matrix(Matrix([[0, 1, 1], [1, 0, 0], [1, 0, 0]]))

Graph.from_vertices_and_edges([0, 1, 2], [(0, 1), (0, 2)])

Graph.from_vertices(range(4))

Graph.from_vertices_and_edges([0, 1, 2, 3], [])

Graph.from_vertices_and_edges(range(6), [[i, (i+2) % 6] for i in range(6)])

Graph.from_vertices_and_edges([0, 1, 2, 3, 4, 5], [(0, 2), (0, 4), (1, 3), (1, 5), (2, 4), (3, 5)])

We can take the union of two graphs:

G = Graph([[0, 1], [1, 2], [2, 0]])
H = Graph([[0, 1], [1, 3], [3, 0]])
G + H

Graph.from_vertices_and_edges([0, 1, 2, 3], [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3)])

G = Graph([[0, 1], [1, 2], [2, 0]])
H = Graph([[3, 4], [4, 5], [5, 3]])
G + H

Graph.from_vertices_and_edges([0, 1, 2, 3, 4, 5], [(0, 1), (0, 2), (1, 2), (3, 4), (3, 5), (4, 5)])

G = Graph.from_vertices_and_edges([0, 1, 2, 3], [[0, 1], [1, 2]])
H = Graph.from_vertices_and_edges([0, 1, 2, 4], [[0, 1]])
G + H

Graph.from_vertices_and_edges([0, 1, 2, 3, 4], [(0, 1), (1, 2)])

A vertex of a graph can be of any hashable type, but it is recommended to have all of them of the same type, not as above. If all vertices have the same type, the vertex/edge set can be sorted when a list is required; otherwise, the order might differ:

G = Graph([[0, 7], [2, 5], [1, 2], [0, 1], [0, 3], [2, 3]])
print(G.vertex_list())
print(G.edge_list())
print(Graph.from_vertices(['a', 1, (1, 2)]).vertex_list())
print(Graph.from_vertices([1, 'a', (1, 2)]).vertex_list())

[0, 1, 2, 3, 5, 7]
[[0, 1], [0, 3], [0, 7], [1, 2], [2, 3], [2, 5]]
['a', 1, (1, 2)]
[1, 'a', (1, 2)]

Alternatively, the adjacency matrix can also be used to construct a graph.

from sympy import Matrix
Graph.from_adjacency_matrix(Matrix([
    [0,1,1],
    [1,0,0],
    [1,0,0]])).plot()

Graph drawer

PyRigi comes with a graph drawer that lets the user input a graph by specifying the vertices (via a click). The edges can be added by dragging the mouse cursor from the head vertex and releasing the click on the tail vertex. Doing so creates an undirected edge.

from pyrigi import GraphDrawer
Drawer = GraphDrawer()

The resulting graph can then be output (and manipulated further) in the following way:

G = Drawer.graph()

Graph database

Alternatively, many common graphs in rigidity theory are already implemented in the graph database graphDB. Graphs from the database can be imported via the following command:

import pyrigi.graphDB as graphs

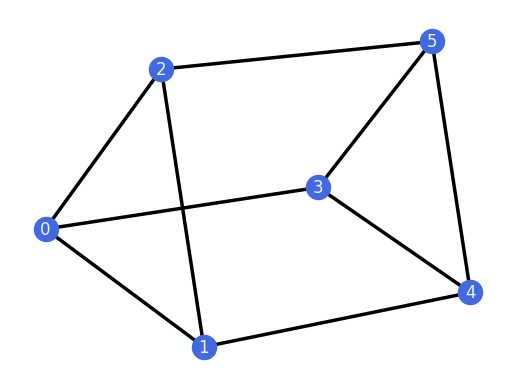
G3 = graphs.ThreePrism()
G3.plot()
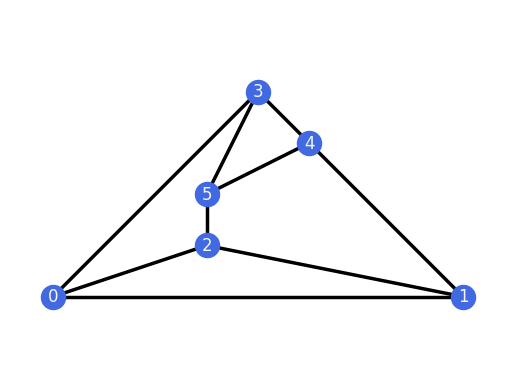
G3.plot(layout="planar")