Using PyRigi for Rigidity Theory

This notebook illustrates how to use PyRigi for applications in rigidity theory using the classes Graph and Framework. It can be downloaded here.

import pyrigi.frameworkDB as frameworks
import pyrigi.graphDB as graphs
from pyrigi import Graph, Framework

Framework Construction

One way to construct a framework is to provide a graph and a realization to the constructor Framework. For instance, a framework F1 on the complete graph on 4 vertices \(K_4\) can be constructed in the following way.

K4 = graphs.Complete(4)

F1 = Framework(K4, {0:[1,2], 1:[0,5], 2:[-1,'1/2 * sqrt(5)'], 3:['1/2','4/3']})
F1

Framework(Graph.from_vertices_and_edges([0, 1, 2, 3], [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)]), {0: ['1', '2'], 1: ['0', '5'], 2: ['-1', 'sqrt(5)/2'], 3: ['1/2', '4/3']})

It is particularly important to provide the numbers as sympy expressions or strings if you intend to perform symbolic computations. Otherwise, fractions are converted to floating point numbers, which may cause issues with the symbolic computation of rigidity properties for the framework. The following example illustrates this behavior.

Framework(graphs.Complete(1), {0:[1/2,2/3]})

Framework(Graph.from_vertices_and_edges([0], []), {0: ['0.500000000000000', '0.666666666666667']})

If you want to use floating point coordinates and you do not specify that the computation should be numeric via the keyword numerical=True in the appropriate methods, then incorrect results may occur.

A framework can then be visualized by calling the method plot() on F1, see also tutorial Plotting.

F1.plot()

The position of a vertex in F1 can be retrieved by calling

F1[2]

\[\begin{split}\displaystyle \left[\begin{matrix}-1\\\frac{\sqrt{5}}{2}\end{matrix}\right]\end{split}\]

Class methods

Alternatively, the realization can be specified by using a class method. For instance, Simplicial() creates a realization on the \(d\)-simplex.

F2 = Framework.Simplicial(K4, 3)
F2

Framework(Graph.from_vertices_and_edges([0, 1, 2, 3], [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)]), {0: ['0', '0', '0'], 1: ['1', '0', '0'], 2: ['0', '1', '0'], 3: ['0', '0', '1']})

The dimension that a framework is embedded in can be accessed via the dim() method.

F2.dim

3

F2[2]

\[\begin{split}\displaystyle \left[\begin{matrix}0\\1\\0\end{matrix}\right]\end{split}\]

The framework can be translated using the translate() method.

F2.translate([3,4,5])

F2[2]

\[\begin{split}\displaystyle \left[\begin{matrix}3\\5\\5\end{matrix}\right]\end{split}\]

Framework database

There exists a framework database from which certain frameworks can be imported. A detailed tutorial of it can be accessed here.

Rigidity properties

Infinitesimal rigidity

One of the main applications of PyRigi is to determine whether a framework is infinitesimally rigid. Take for example the following realization of the 3-prism. We can determine whether it is infinitesimally rigid using the method is_inf_rigid().

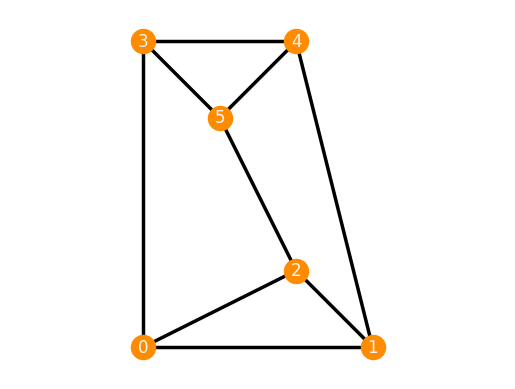
TP_rigid = frameworks.ThreePrism()
TP_rigid.plot()
TP_rigid.is_inf_rigid()

True

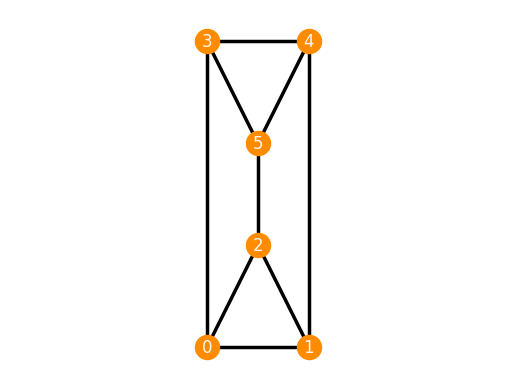
We can also create an infinitesimally flexible, but continuously rigid realization of the 3-prism using the parameter 'parallel'.

TP_parallel = frameworks.ThreePrism('parallel')
TP_parallel.plot()
TP_parallel.is_inf_rigid()

False

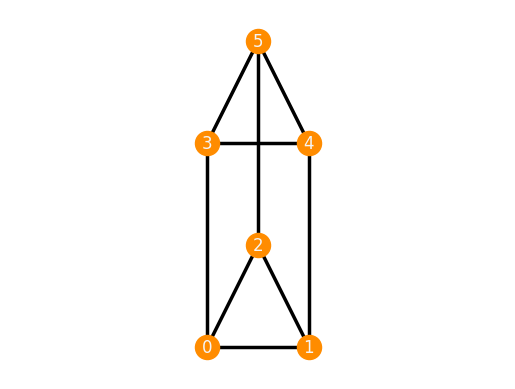
We check its rigidity using the method is_inf_rigid(). Finally, a continuously flexible realization can be created using the keyword 'flexible'.

TP_flexible = frameworks.ThreePrism('flexible')
TP_flexible.plot()
TP_flexible.is_inf_rigid()

False

Adding an edge to the 3-prism changes its rigidity properties.

TP_e = frameworks.ThreePrismPlusEdge()
TP_e.plot()
TP_e.is_inf_rigid()

True

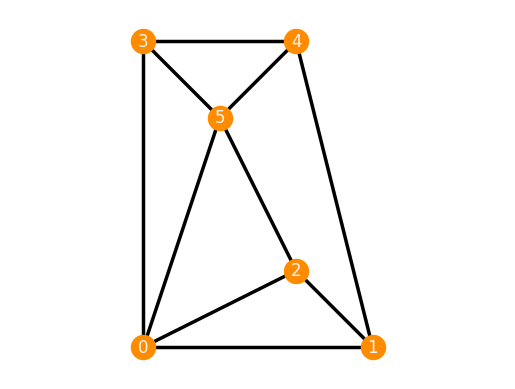
In particular, the resulting framework is not minimally infinitesimally rigid anymore, even though the 3-prism was.

print(TP_rigid.is_min_inf_rigid())
print(TP_e.is_min_inf_rigid())

True
False

To investigate further properties of the framework, PyRigi can be used for computing the corresponding rigidity matrix using the method rigidity_matrix().

TP_flexible.rigidity_matrix()

\[\begin{split}\displaystyle \left[\begin{array}{cccccccccccc}-2 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\-1 & -2 & 0 & 0 & 1 & 2 & 0 & 0 & 0 & 0 & 0 & 0\\0 & -4 & 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0 & 0 & 0\\0 & 0 & 1 & -2 & -1 & 2 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & -4 & 0 & 0 & 0 & 0 & 0 & 4 & 0 & 0\\0 & 0 & 0 & 0 & 0 & -4 & 0 & 0 & 0 & 0 & 0 & 4\\0 & 0 & 0 & 0 & 0 & 0 & -2 & 0 & 2 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0 & 0 & -1 & -2 & 0 & 0 & 1 & 2\\0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -2 & -1 & 2\end{array}\right]\end{split}\]

If you do not want to compute the infinitesimal flexes on your own, you can ask PyRigi to do it. The method nontrivial_inf_flexes() returns a list of nontrivial infinitesimal flexes that all in the format of a matrix.

inf_flexes = TP_flexible.nontrivial_inf_flexes()
inf_flexes[0]

\[\begin{split}\displaystyle \left[\begin{matrix}1\\0\\1\\0\\1\\0\\0\\0\\0\\0\\0\\0\end{matrix}\right]\end{split}\]

We can verify that a vector is indeed an nontrivial infinitesimal flexes by calling the method is_nontrivial_flex().

print(TP_flexible.is_nontrivial_flex(inf_flexes[0]))
print(TP_rigid.is_nontrivial_flex(inf_flexes[0]))

True
False

The list of trivial infinitesimal flexes can be accessed via the method trivial_inf_flexes().

inf_flexes = TP_flexible.trivial_inf_flexes()
inf_flexes[0]

\[\begin{split}\displaystyle \left[\begin{matrix}1\\0\\1\\0\\1\\0\\1\\0\\1\\0\\1\\0\end{matrix}\right]\end{split}\]

Equilibrium Stresses

PyRigi can also be used to compute equilibrium stresses. This is done via the method stresses().

F = frameworks.Frustum(3)
inf_flex = F.inf_flexes()[0]
stress = F.stresses()[0]
stress

\[\begin{split}\displaystyle \left[\begin{matrix}-2\\-2\\-6\\-2\\-6\\-6\\1\\1\\1\end{matrix}\right]\end{split}\]

We can visualize both the infinitesimal flexes and equilibrium stresses of a framework by using the appropriate keywords.

F.plot(inf_flex=inf_flex, stress=stress)

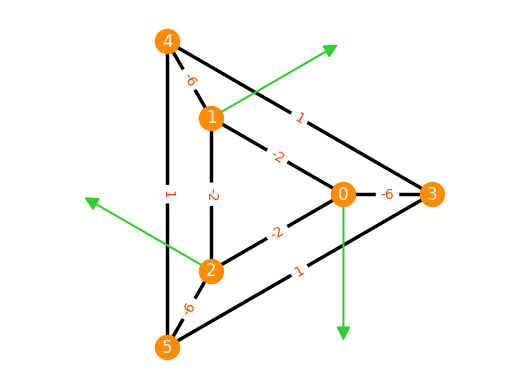
Again, it can be verified that the stress indeed lies in the cokernel of the rigidity matrix by calling is_stress().

F.is_stress(stress)

True

The stress matrix associated to a framework for a given stress can be accessed via the method stress_matrix().

Omega = F.stress_matrix(stress)

Generic rigidity

We can also use PyRigi to investigate the generic rigidity of graphs. The underlying graph of a framework can be accessed via the property Framework.graph and the rigidity of this graph can be determined via is_rigid().

G_TP = TP_rigid.graph
G_TP.is_rigid()

True

The dimension in which its rigidity is supposed to be investigated can be specified via the dim keyword.

G_TP.is_rigid(dim=1)

True

For dimensions greater than 2, no combinatorial rigidity criterion is known. To still get a result, a randomized algorithm can be called using the command:

G_TP.is_rigid(dim=3, algorithm="randomized")

False

In fact, we can compute the maximal dimension, in which a graph is rigid using the method max_rigid_dimension(). This method uses a randomized algorithm to determine rigidity in an arbitrary dimension, so it throws a RandomizedAlgorithmWarning. To silence it, we can set Graph.silence_rand_alg_warns=True.

Graph.silence_rand_alg_warns = True
G_TP.max_rigid_dimension()

2

Furthermore, we can compute the rigid components of a graph using rigid_components(), which is returned as a partition of vertices.

G = graphs.DoubleBanana()
G.rigid_components(dim=3, algorithm="randomized")

[[0, 1, 2, 3, 4], [0, 1, 5, 6, 7]]

We can also investigate the (generic) (global) rigidity of a graph using the method is_globally_rigid():

G_TP.is_globally_rigid()

False

and

G4 = graphs.ThreePrismPlusEdge()
G4.plot()
G4.is_globally_rigid()

True

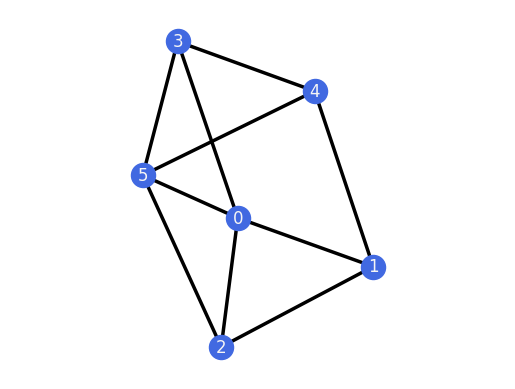
To distinguish graphs from frameworks in the plot() method, the vertices are colored differently by default. The graph G4 obtained by adding an edge to the 3-prism is globally rigid because it is 3-connected and redundantly rigid. The redundant rigidity of a graph can be checked via is_redundantly_rigid().

G4.is_redundantly_rigid()

True

We can also investigate the global rigidity for other dimensions, too.

G_TP.is_globally_rigid(dim=1)

True

Finally, it may be useful to check whether a graph can be constructed via an extension sequence, which can be done using the method extension_sequence().

for H in G_TP.extension_sequence(return_type="graphs"):
    H.plot(canvas_height=2)

We can obtain all non-isomorphic \(k\)-extensions of a graph using the method all_k_extensions(). For the 3-prism we ensure that all of the 0-extensions are rigid:

for H in G_TP.all_k_extensions(0, only_non_isomorphic=True):
    H.plot()
    assert(H.is_rigid())

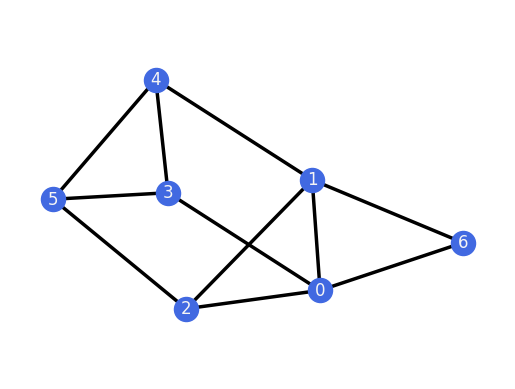
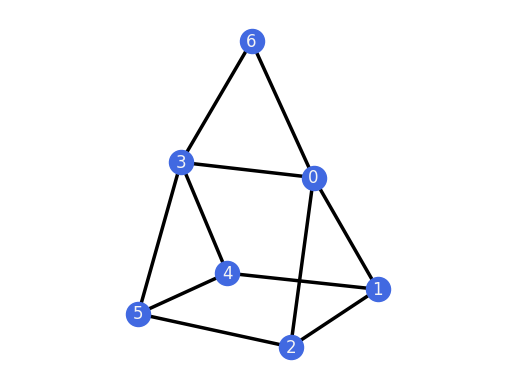
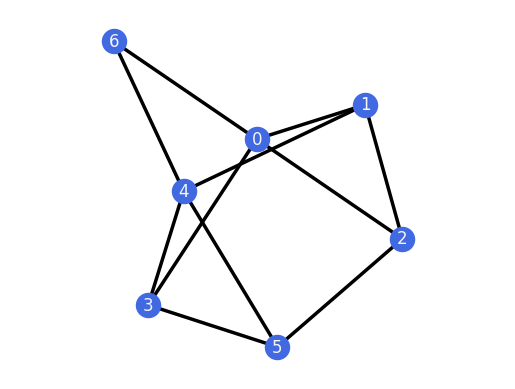
And we can do the same for the 1-extensions of the 3-prism.

for H in graphs.ThreePrism().all_k_extensions(1, only_non_isomorphic=True):
    H.plot()
    assert(H.is_rigid())

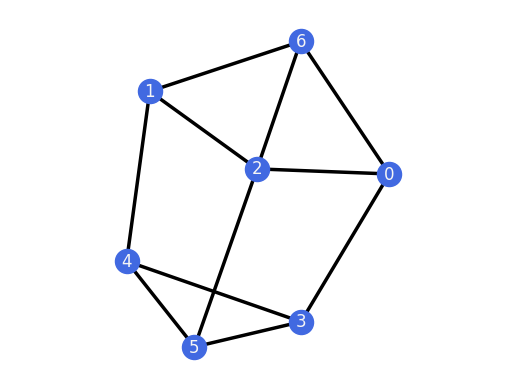
Sparsity

The (k,l)-sparsity of a graph can be checked using the method is_kl_sparse().

G = graphs.CompleteBipartite(3,3)
G.is_kl_sparse(2, 3)

True

Famously, the double banana is (3,6)-sparse, but not rigid.

G = graphs.DoubleBanana()
print(G.is_kl_sparse(3, 6))
print(G.is_rigid(dim=3, algorithm="randomized"))

True
False

Similarly, it can be checked whether a graph is (k,l)-tight.

TP = graphs.ThreePrism()
TP.is_kl_tight(2, 3)

True

Matroidal Properties

We can use PyRigi to check properties of graphs in the d-dimensional rigidity matroid as well. To check whether a graph is (in-)dependent in this matroid, we can call is_Rd_dependent() or is_Rd_independent().

TP.is_Rd_independent()

True

It can be checked whether a graph is a circuit in the d-dimensional rigidity matroid by calling is_Rd_circuit().

TP.is_Rd_circuit()

False

Finally, it can be determined whether the graph is \(R_d\)-closed by calling is_Rd_closed().

TP.is_Rd_closed(dim=1)

False